Solusi SPL & Transformasi Linear

Sebelum kita masuk ke solusi SPL, sebelumnya kita harus tahu bahwa SPL itu dibagi menjadi 2 jenis, yaitu:

A. Sistem Persamaan Linear Homogen

Sistem Persamaan Linear Homogen adalah sistem persamaan linear yang semua sukukonstannya nol sehingga bentuk umum SPL homogen ini sebagai berikut:
a11x1+a12x2+ … + a1nxn= 0
a21x1+ a22x2+ … + a2nxn= 0
. . . .
. . . .
am1x1+ am2x2+ . . . + amnxn= 0

SPL homogen selalu konsisten, minimal mempunyai penyelesaian nol(x1, x2, … , xn=0) disebut Penyelesaian Trivial. Jika di SPL tersebut mempunyai penyelesaian yang banyak, penyelesaian tersebut disebut Penyelesian Tak Trivial. Dalam SPL Homogen terdapat teorema, teorema itu adalah : Sistem persamaan linear homogen selalu mempunyai penyelesaian tak trivial, jika banyaknya variabel lebih besar dibandingkan banyaknya persamaan.

B. Sistem Persamaan Linear Non-Homogen

Sebuah sistem persamaan linier dapat dikatakan nonhomogen apabila mempunyai bentuk :
a11x1+a12x2+ … + a1nxn= b1
a21x1+ a22x2+ … + a2nxn= b2
. . . .
. . . .
am1x1+ am2x2+ . . . + amnxn= bm

Terdapat teorema bahwa di SPL non homogen, x(x1, x2, …, xn)≠0

Ada 3 kemungkinan pemecahan SPL Non Homogen, yaitu:

a. Tidak mempunyai penyelesaian

b. Mempunyai tepat satu penyelesaian

c. Mempunyai tak hingga banyaknya penyelesaian

Macam-Macam Solusi SPL

1. 1. Metode Eliminasi

Metode eliminasi adalah salah satu metode yang sederhana, yaitu dengan cara menghilangkan suatu atau beberapa variabel dari semua persamaan yang lain, sehingga diperoleh nilai dari variabel yang kita inginkan. Setelah itu mensubstitusikan nilai variabel yang telah kita peroleh tersebut ke dalam persamaan-persamaan lain sehingga diperoleh nilai variabel-variabel lainnya.
2. Aturan Cramer

Jika AX = B adalah sistem yang terdiri dari n persamaan linier dalam n bilangan tak diketahui sehingga det(A) 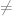 0, maka sistem tersebut mempunyai pemecahan yang uniq. Pemecahan ini adalah x1=  x2= xn=

3. Aturan Gauss

Eliminasi Gauss adalah suatu metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana lagi. Dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.

Ciri ciri Metode Gauss adalah

1. Jika suatu baris tidak semua nol, maka bilangan pertama yang tidak nol adalah 1 (1 utama)
2. Baris nol terletak paling bawah
3. 1 utama baris berikutnya berada dikanan 1 utama baris diatasnya
4. Dibawah 1 utama harus nol

4. Aturan Gauss-Jordan

Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana lagiCaranya adala. h dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks.

Metode ini digunakan untuk mencari invers dari sebuah matriks.

Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah

1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.

2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks

A menjadi dalam bentuk baris eselon yang tereduksi.

CONTOH SOAL INVERS MATRIKS

CONTOH SOAL METODE CRAMER

CONTOH SOAL METODE GAUS

CONTOH SOAL METODE GAUSS-JORDAN

Dalam bagian ini kita mulai mempelajari fungsi bernilai vektor dari sebuah peubah vektor. Yakni, fungsi yang berbentuk w = F(v), dimana baik peubahbebas v maupun peubah tak-bebas w adalah vektor. Kita akan memusatkan perhatian pada kelompok khusus fungsi vektor yang kita namakantransformasi linear. Kelompok fungsi ini mempunyai banyak penerapan penting dalam fisika, bidang teknik, ilmu sosial, dan berbagai cabang matematika.

Jika V dan W adalah ruang vektor dan F adalah sebuah fungsi yang mengasosiasikan vektor unik di W dengan setiap vektor terletak di V, maka kita katakana Fmemetakan V ke dalam W, dan kita tuliskan F:VàW. lebih lanjut lagi, jika Fmengasosiasikan vektor w dengan vektor v, maka kita tuliskan w = F(v) dan kita katakan bahwa w adalah bayangan dari v di bawah F. ruang vektor V dinamakan domainF.

Untuk melukiskannya, jika v = (x,y) adalah sebuah vektor di R², maka rumusnya

Mendefenisikan sebuah fungsi yang memetakan R² ke dalam R³. Khususnya jika v = (1,1), maka x = 1 dan y = 1, sehingga bayangan dari v di bawah F adalah F(v) = (1,2,0) dengan demikian , domain F adalah R².

Defenisi, jika F:V W adalah sebuah fungsi dari ruang vektor V ke dalam ruang vektor W, maka F kita namakan transformasi linear ( linear transformasi) jika

(i) F(u + v) = F (u) + F (v) untuk semua vektor u dan v di V.

(ii )F(ku) = kF(u) untuk semua vektor u di dalam V dan semua skalar k.

Untuk melukiskannya, misalnya F:R²àR³ adalah fungsi yang didefinisikan oleh pers. 1, , sehingga

            

Demikian juga, jika k adalah sebuah skalar, ku = (kx₁, ky₁), sehingga

Jadi, F adalah sebuah transformasi linear.

Jika F:VàW adalah sebuah transformasi linear, maka untuk sebarang v₁ dan v₂ di V dan sebarang skalar k₁ dan k₂, kita peroleh

Demikian juga, jika v₁, v₂, ……,v_n adalah vektor-vektor di V dan k₁, k₂,…….k_n adalah skalar.